Perspective-vue
Designing a 2D game for a 2D screen is pretty simple to us. But it comes to design a 3D environment for a 2D computer screen we tend to adopt game engines thinking that's a lot of complex math we can't handle. Though there's no denying the reliability of game engines, some features of the 3D environment can be implemented with really simple mathematics we learnt at school. This repository is intented to demonstrate that.

Perspective drawing is a drawing technique used to illustrate dimension through a flat surface. This is how we see a flat surface image and perceive a 3D environment in our brain depending on the position and sizes of the objects drawn. So if we can do the math to calculate how large or small the object needs to be drawn depending on how far it is from the screen, that's all we need to have a 3D layout.
Getting Started
This is a vue app, clone the repository, set it up, play around.
Project setup
yarn install
Compiles and hot-reloads for development
yarn run serve
Compiles and minifies for production
yarn run build
Lints and fixes files
yarn run lint
The Math
Let's see how easy the math is.
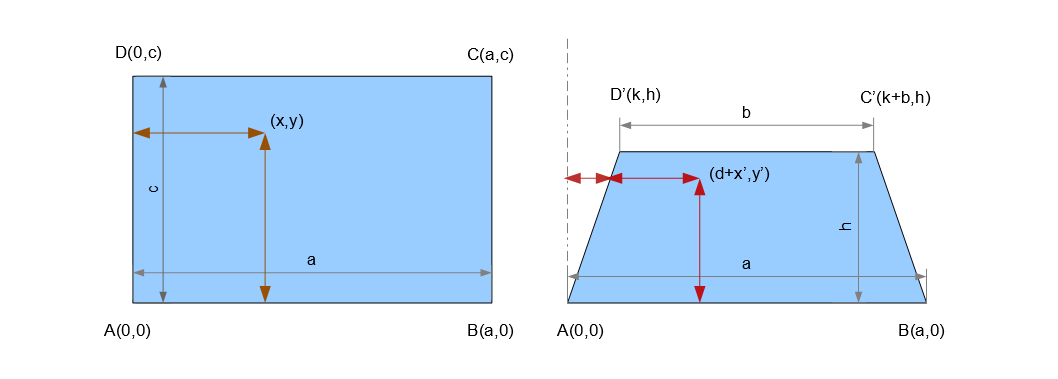
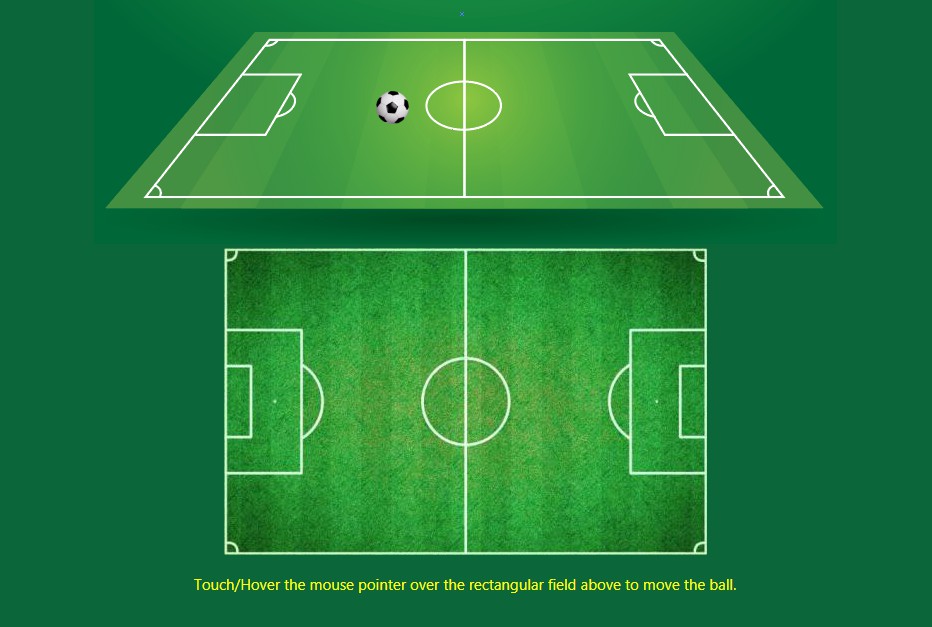
On the left we have a 2D view of a football field and on the right a 3D perspective drawing
of the same field. In your mind it has 3 axes (x, y, z) but the paper you would be drawing
on has only 2 axes just like the first one and (x', y') is the point on that paper that
represents the point (x, y) on the left figure. There is no z-axis on drawing paper, so
what appears to be the z-axis on the right figure is actually the y-axis of the paper.
So if you look closely the point on the right figure that represents (x, y) is actually
(d + x', y') with respect to the drawing paper where d is the displacement due to the
shifting of left side of the rectangle from the y-axis.
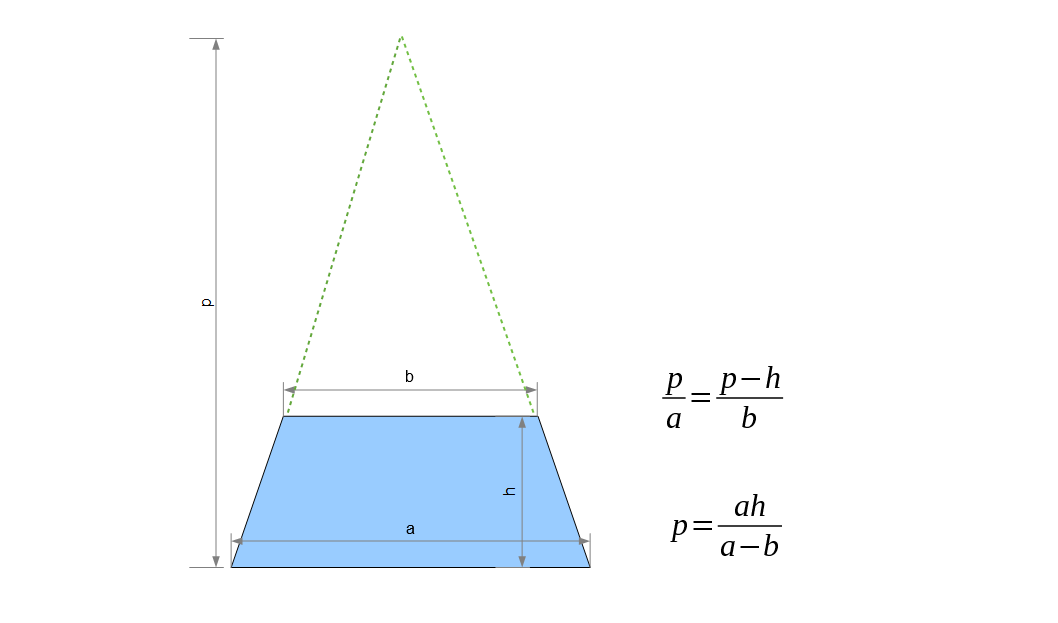
If we extend the unparallel sides of the trapeze backwards they meet at a point of
projection P which is at infinity distance from the screen. Say the point is at a height p
from x-axis on the drawing paper. We can calculate the length of p from the two similar
triangles in the figure below.
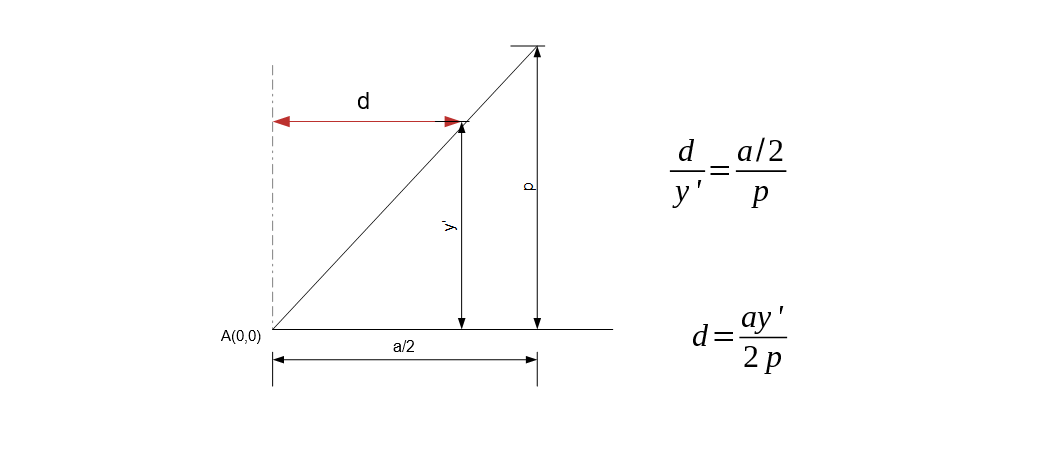
Comparing similar triangles we can calculate the value of d from the following figure.
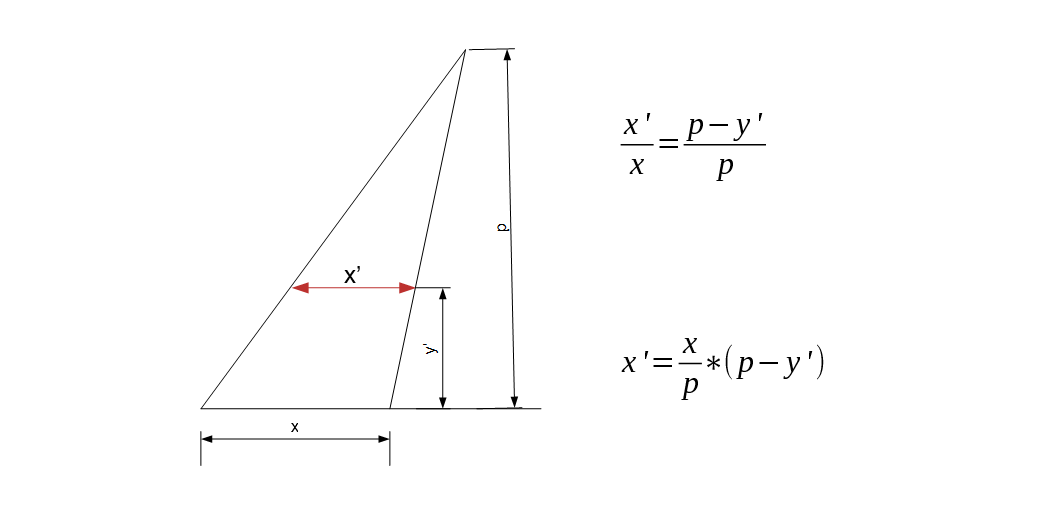
Now let's calculate the size of objects at different distances from the viewer. Any object
which appears to be of length x when positioned at the x-asis will appear smaller when we
move it away from the screen. Say it appears to be of length x' when positioned at a
distance y' from x-axis on the drawing paper (y' is not equal to y, it is the height on
the paper where x' is drawn which we will calculate in next step). So we calculate the value
of x' at a distance y' comparing the two similar triangles in the following figure.
Now calculating the value of y' is slightly complicated. If an object is in the middle of the
2D space, it won't be in the middle of the 3D space drawn on a 2D screen/paper.
For better understanding we squeeze the height of the rectangle to match that of the the trapezium.
The middle point of both the field is where the diagonals meet and they don't meet at the same height
on the drawing paper.
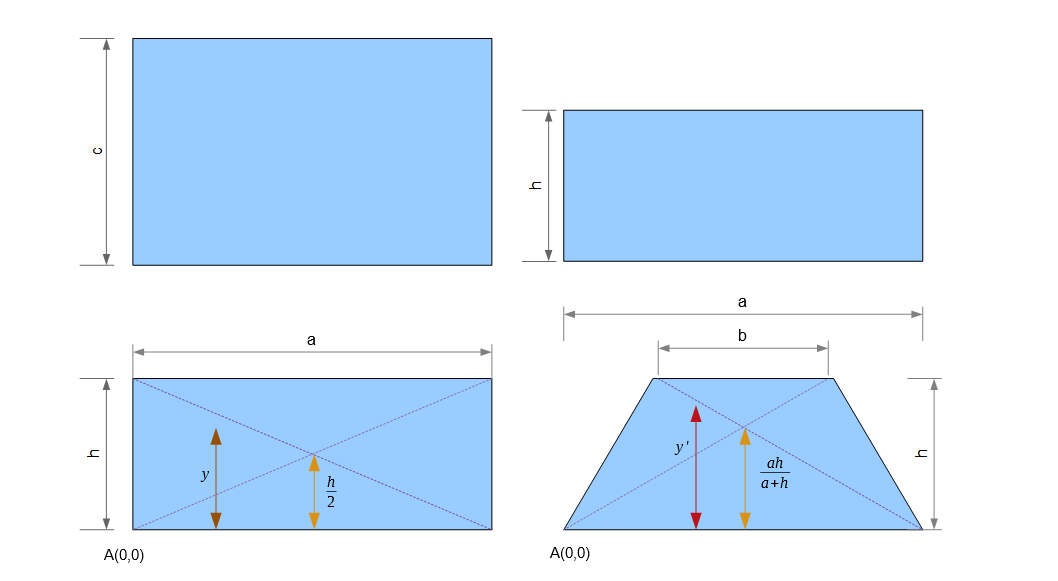
The following table shows corresponding values of y' with respect to y.
| y | y' |
|---|---|
| 0 | 0 |
| h/2 | ah/(a+h) |
| h | h |
| ∞ | p |
The ratio of distances of y' from a and b is proportional to the lengths of a and b.
The relationship is illustrated in the figure below.
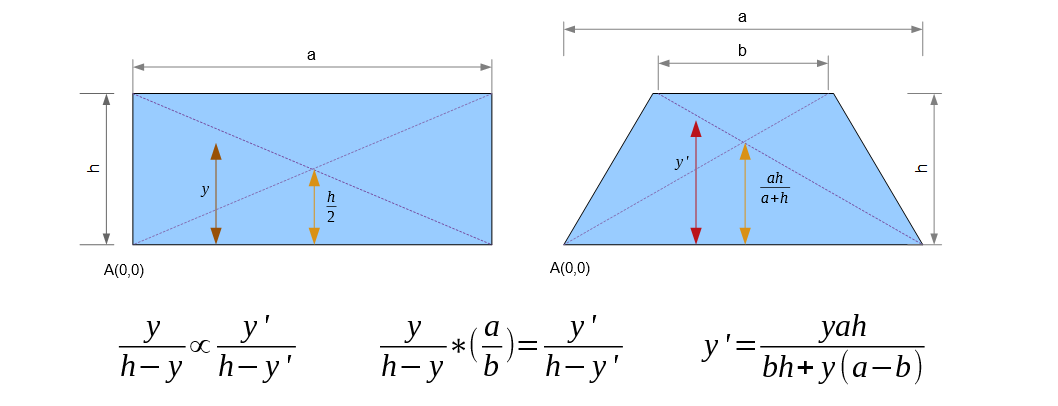
This equation satisfies all the corresponding values shown in the table above. If you get stuck
verifying the last one, the trick is the term bh is negligible to the term ∞(a-b)
and thus can be taken off the equation.
Acknowledgments
This repository is just intended to demonstrate use of simple math to solve complex looking challenges.