Prompts Royale
Prompt engineering is an extremely iterative process. Even when we manage to settle down on a prompt, it’s so difficult to test it against test cases and other possible prompts to make sure we’re giving the best instructions to the model.
Prompts Royale is an application that allows you to really easily create many prompt candidates, write your own ones, and make them battle until a clear winner emerges. It makes the process of iterating on a prompt feel much more easy and reliable.
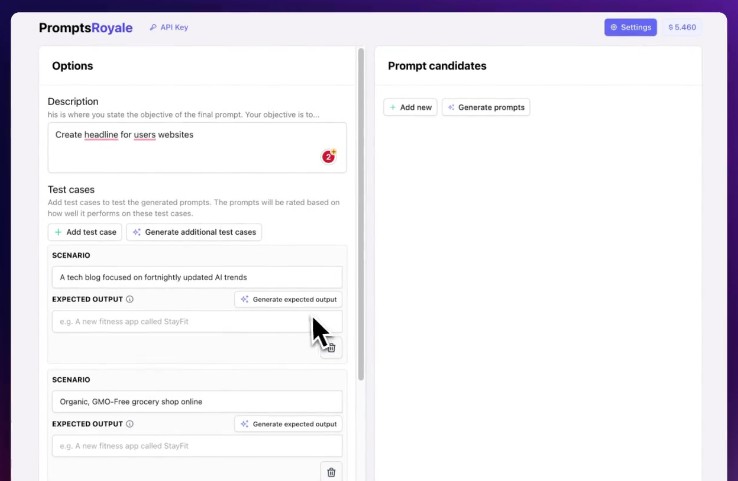
You give a description of what you want to accomplish, give it a few scenarios and expected outputs, and then just sit back and watch them battle for #1.
prompts.royale.mp4
What it can do
- Automatic prompt generation: Allows for the creation of prompt candidates from the user’s description and test case scenarios. The user can also input their own.
- Automatic test cases generation: Enables automatically creating test cases from the description to get the juices flowing!
- Monte Carlo Matchmaking + ELO Rating: It uses the Monte Carlo method for matchmaking to ensure you get as much information with the least amount of battles, and ELO Rating to properly rank candidates based on their wins and who they win against
- Everything is customizable: The settings page allow you to tinker with every single parameter of the application
- Local & Secure: Everything is stored locally and requests are made from your browser to the LLMs API.
Usage
You can use it at promptsroyale.com, or you can clone the repository and run it locally.
Clone the repository:
git clone ssh://github.com/meistrari/prompts-royale.git
Install the dependencies:
npm install
Run the server:
npm run dev
Example
Here’s an example of what a use case would look like:
Description
Write a prompt that creates a headline for a website.
Example 1
Scenario
Website of a car dealership
Expected Output
Find the car of your dreams at the best price
Example 2
Scenario
Website of a SaaS for data analytics
Expected Output
Your data, your insights, your way
Example 3
Scenario
Website for a zoo
Expected Output
Animals of the world, in one place
With the information of the task to be accomplished and the test cases, the user can then Generate prompt candidates, that take those into account and outputs N candidates that will be ranked by the system through a combat system.
The user can also write the prompt candidates themselves if they have a specific idea of what they want. If you have something specific in mind, writing your prompts is always the best option to fit what you intend.
Click to see an example of the generated prompts
Prompt A
Design a compelling headline for a distinct category of website. Understand the website’s mission, its intended audience, and the solutions it provides. The headline should attract attention, be pertinent, and distill the website’s core concept into a succinct statement. Leverage your linguistic proficiency, promotional tactics, and domain-specific knowledge to create an enticing headline.”
Prompt B
Your directive is to formulate an attractive headline for a specific kind of website. Pay attention to the website’s objectives, its targeted demographics, and the services it offers. The headline should be captivating, germane, and capable of summarizing the website’s primary proposition in a brief line. Use your language comprehension, advertising strategies, and industry-specific insights to create a compelling headline.
How It Works
Each prompt is represented as a normal distribution with an initial mean $\mu$ of $1000$ and a standard deviation $\sigma$ of $350$. This distribution represents the ELO score of the prompt.
We then repeat the following cycle:
We use a monte carlo sampler to make duels where each of the 2 selected prompts battle each other. The chances of being drawn for the duel are proportional to the chance that that prompt is the best, or in more mathematical terms, we use the weighted distribution of their probability density to define the likelihood that that curve has the highest true mean within the group.
In each duel, both prompts answer each of the test cases and a separate prompt evaluates which answer was the best. The ELO scores of the prompts are then updated according to the following formulas:
$$\mu_{A}’ = \mu_{A} + \frac{K}{N} \cdot (score – expected\_score(A,B))$$
$$\mu_{B}’ = \mu_{B} + \frac{K}{N} \cdot (1 – score – expected\_score(B,A))$$
$$\sigma_{A}’ = \sigma_{A} \cdot LR$$
$$\sigma_{B}’ = \sigma_{B} \cdot LR$$
Where:
-
$LR$ is the learning rate. The lower the learning rate the faster the “learning”. By decreasing the standard deviation, you make results more meaningful. This means that the system will converge faster to a winner, but it also means that it will be less likely to find the best result. We recommend $0.96$.
-
$K$ is the number of points each battle has at stake.
-
$N$ is the number of test cases
-
$\dfrac{K}{N}$ is the amount of points each round has at stake
- If two prompts with the same $\mu$ battle and one prompt wins all of the rounds it will gain $\dfrac{K}{2}$ points and the other will lose $\dfrac{K}{2}$ points.
-
$score$ is $1$ if $A$ wins and $0$ if $B$ wins,
-
$expected\_score(A,B)$ is the expected chance of $A$ winning of $B$ given their normal distributions. This is calculated by the following formula: $$expected\_score(A,B) = \frac{1}{1 + 10^{\frac{\mu_{B} – \mu_{A}}{400}}}$$
The reason why we update the $\sigma$ of each prompt is that we have more certainty on the distribution after each match, thus it should have a smaller standard deviation.
Credits
We were heavily inspired by https://github.com/mshumer/gpt-prompt-engineer, thanks for your work!